Curves and Surfaces

The goal of this assignment is to get you to think about what you've learned about tensor-product curves and subdivision curves and surfaces.

So, the questions aren't so much for you to answer, but rather, for you to think about and make sure that you would know how to answer.

We will not check your answers. We will take your word that you did the work. If you do the work (e.g. think through the assignment), and just hand in a piece of paper saying "I did the work," you will get credit. You should actually think about the questions though, since they may appear again on an exam.

Question 1:

For curves, the B-Splines look like bumps. What do tensor product B-Splines look like for surfaces?

Consider the B-Spline for uniform (periodic) knots for order d=2 (on page 22 of the notes). B-Spline 0 for this is the one in the lower left of figure 8 - the "hat" centered around 1. What would the formula for this (as a function of u) be? What would the formula for the 2D B-Spline "0,0" (as a function of u and v) be?
(you can either figure this out by using the cox-deboor recurrance, or by just looking at the picture)

Question 2:

Most tensor product surfaces such as Bilinear patches or B-Splines are defined over rectangular patches. Why might patches defined over triangles be more convenient?

If you make a "sheet" of tensor-product surfaces (such as a B-Spline), you need to have a regular grid of control points. What happens when you want to make a more complex shape that a single sheet can't be folded into?

Question 3:

Consider subdivision curves. We'll denote the ith point on the "k-th" level of the curve as

So, we could define a line as: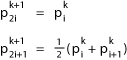
(convince yourself that this does create a connected set of line segments)

Here's another type of subdivision curve (the parameter w is a tension parameter that is almost always set equal to 1/16):

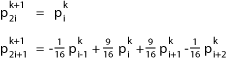
This curve is called a "4 point scheme" (why?). Try to figure out the shape it has by thinking of what it would take to implement it. Then, go to the web page at Caltech http://www.multires.caltech.edu/teaching/demos/java/4point.htm and read more about it and see how it behaves.

You should also look at this demo.

Question 4:

Much like with tensor product surfaces, subdivision schemes work "best" on regular grids, but have rules for what to do at extraordinary points.

Draw a "triangle grid" and draw extra points on the line segments that could be divided using the "ordinary" rules for Butterfly subdivision.

Consider a cube. Think of various ways of breaking it into triangles - do any lead to "regular" triangle meshes for butterfly schemes?

Question 5:

Even if things are made out of squares, they may not be enough of a regular grid to work with tensor product surfaces or Catmull-Clark Subdivision surfaces.

Consider a cube. Without re-using points, could this be used with "ordinary" Catmull-Clark (or B-Spline) rules?

If you subdivide the entire cube once using the Catmull-Clark, how many extra-ordinary points remain?