Detecting Manipulated Remote Call Streams

Abstract

In the Internet, mobile code is ubiquitous and includes such examples as browser plug-ins, Java applets, and document macros. In this paper, we address an important vulnerability in mobile code security that exists in remote execution systems such as Condor, Globus, and SETI@Home. These systems schedule user jobs for execution on remote idle machines. However, they send most of their important system calls back to the local machine for execution. Hence, an evil process on the remote machine can manipulate a user's job to send destructive system calls back to the local machine. We have developed techniques to remotely detect such manipulation.

Before the job is submitted for remote execution, we construct a model of the user's binary program using static analysis. This binary analysis is applicable to commodity remote execution systems and applications. During remote job execution, the model checks all system calls arriving at the local machine. Execution is only allowed to continue while the model remains valid. We begin with a finite-state machine model that accepts sequences of system calls and then build optimizations into the model to improve its precision and efficiency. We also propose two program transformations, renaming and null call insertion, that have a significant impact on the precision and efficiency. As a desirable side-effect, these techniques also obfuscate the program, thus making it harder for the adversary to reverse engineer the code. We have implemented a simulated remote execution environment to demonstrate how optimizations and transformations of the binary program increase the precision and efficiency. In our test programs, unoptimized models increase run-time by 0.5% or less. At moderate levels of optimization, run-time increases by less than 13% with precision gains reaching 74%.

1. Introduction

Code moves around the Internet in many forms, including browser plug-ins, Java applets, document macros, operating system updates, new device drivers, and remote execution systems such as Condor [26], Globus [13,14], SETI@Home [32], and others [1,11,35]. Mobile code traditionally raises two basic trust issues: will the code imported to my machine perform malicious actions, and will my remotely running code execute without malicious modification? We are addressing an important variant of the second case: the safety of my code that executes remotely and makes frequent service requests back to my local machine (Figure 1). In this case, we are concerned that a remotely executing process can be subverted to make malicious requests to the local machine.

The popular Condor remote scheduling system [26] is an example of a remote execution environment. Condor allows a user to submit a job (program), or possibly many jobs, to Condor to run on idle machines in their local environment and on machines scattered worldwide. Condor jobs can execute on any compatible machine with no special privilege, since the jobs send their file-access and other critical system calls to execute on their home machines. The home or local machine acts as a remote procedure call (RPC) server for the remote job, accepting remote call requests and processing each call in the context of the user of the local system. This type of remote execution, with frequent interactions between machines, differs from execution of "mobile agents" [17,30], where the remote job executes to completion before attempting to contact and report back to the local machine.

If the remote job is subverted, it can request the local machine to perform dangerous or destructive actions via these system calls. Subverting a remote job is not a new idea and can be done quickly and easily with the right tools [16,27]. In this paper, we describe techniques to detect when the remote job is making requests that differ from its intended behavior. We are addressing the issue of the local host's safety; we are not protecting the remote job from inappropriate access to its data nor are we detecting modification of its calculated result (beyond those which would appear as inappropriate remote system calls).

A local machine that accepts calls as valid without first verifying that the remote job generated the calls during correct execution is vulnerable to maliciously generated calls. Conventional authentication methods using secret data fail in this inherently risky environment. An attacker knows everything present in the remote code, including an authentication mechanism or key, and can manipulate this code at will. Thus, although the local machine must distrust calls from remotely executing code, it has little ability to validate these requests. This vulnerability currently exists in the thousands of machines worldwide running Condor, Globus, Java applets, and similar systems. Our techniques address this deficiency.

Our basic approach to detecting malicious system call streams is to perform a pre-execution static analysis of the binary program and construct a model representing all possible remote call streams the process could generate. As the process executes remotely, the local agent operates the model incrementally, ensuring that any call received remains within the model. Should a call fall outside the set of expected next calls determined by the model, we consider the remote process manipulated. Reasonably, a precise model should closely mirror the execution behavior of the application.

As others have noticed [23,36,37], specification of a program's intended behavior can be used for host-based intrusion detection. Our approach brings four benefits to these intrusion detection systems:

• Direct operation on binary code.
• Automated construction of specifications.
• Elimination of false alarms.
• Protection against new types of attacks.

We further address an important new source of vulnerabilities: request verification when even cryptographic authentication mechanisms cannot be trusted.

Any program model representing sequences of remote system calls is valid. Previous model construction techniques include human specification [22] and dynamic analysis. A dynamic analyzer completes training runs over multiple execution traces to build probability distributions indicating the likelihood of each call sequence [12,15,39]. False alarms occur if the training runs do not exercise all possible program control flows. Static analysis produces non-probabilistic models representing all control flow paths through an executable. These models are conservative, producing no false alarms [36,37] but potentially accepting an attack sequence as valid.

Our models are finite-state machines. We use control flow graphs generated from the binary code under analysis to construct either a non-deterministic finite-state automaton or a push-down automaton to mirror the flow of control in the executable. Automata are natural structures to represent sequences of remote call names, with push-down automata being more precise. We develop several optimizations to further increase precision while maintaining run-time efficiency.

We evaluate our program models using two metrics: precision and efficiency. Precision measures how tightly the model fits the application it represents. Improving precision reduces the opportunity for an attack to be accepted as valid by the model. Efficiency rates the run-time impact of model operation. To evaluate our techniques and models, we built a prototype static analyzer and model builder for a simulated remote execution environment. We read binary programs on SPARC Solaris machines and produce a model for operation by a simulated local agent. The agent receives notifications from the application when system calls are encountered during execution and operates the model accordingly.

Our models are efficient. Non-deterministic finite-state automaton (NFA) models add 0.5% or less to the run-times of our test applications. In the less precise NFA models, optimizations become invaluable. Moderate optimization levels improve precision up to 74% while keeping run-time overheads below 13%. Optimized push-down automaton models are more precise, but keep overheads as low as 1%. The precision values of these optimized models approach zero, indicating little opportunity for an adversary to begin an attack.

Other strategies have been used to counter mobile code manipulation exploits. Generally orthogonal, one finds the greatest security level when incorporating components of all three areas into a solution.

Replication. A form of the Byzantine agreement [24], a remote call will be accepted as genuine if a majority of replicated processes executing on different machines generate the identical call. Sometimes used to verify the results returned by mobile agents [31], such techniques appear limited in an environment with frequent system call interactions over a wide network.

Obfuscation. A program can be transformed into one that is operationally equivalent but more difficult to analyze [7,8,30,38]. We are applying a variant of such techniques to improve our ability to construct precise state machines and hamper an adversary's ability to understand the semantics of the program. Even though it has been popular in recent years to discount obfuscation based upon Barak et. al. [5], in Section 3.4.2 we discuss why their theoretical results do not directly apply in our context.

Sandboxing. Running a program in an environment where it can do no harm dates back to the early days of the Multics operating system project [29]. CRISIS, for example, maintains per-process permissions that limit system access in WebOS [6]. Our techniques could be considered a variety of sandboxing, based on strong analysis of the binary program and construction of a verifying model to support that analysis.

This paper makes contributions in several areas:

Binary analysis. We target commodity computational Grid environments where the availability of source code for analysis cannot be assumed. Further, our analysis is not restricted to a particular source language, so our techniques have wide applicability.

Model optimizations. We develop and use techniques to increase the precision of the finite-state machines we generate, limiting the opportunities for an attacker to exploit a weakness of the model. In particular, we reduce the number of spurious control flows in the generated models with dead automata removal, automata inlining, the bounded stack model, and the hybrid model. Argument recovery reduces opportunities for exploit. We also present a linear time ε-reduction algorithm to simplify our non-deterministic state machines.

Reduced model non-determinism with obfuscatory benefits. Many different call sites in a program generate requests with the same name. (All opens, for example.) Our technique of call site renaming gives us a great ability to reduce the non-determinism of our models by uniquely naming every call site in the program and rewriting the executable. We further insert null calls-dummy remote system calls-at points of high non-determinism to provide a degree of context sensitivity to the model. Call site renaming and null call insertion additionally obfuscate the code and the remote call stream. With binary rewriting, other obfuscation techniques are likewise possible.

Context-free language approximations. In general, the language generated by the execution trace of a program is context-free. A push-down automaton-a finite-state machine that includes a run-time stack-defines a context-free language. However, such automata are prohibitively expensive to operate incrementally [36,37] and stack growth potentially consumes all system resources. We use stack abstractions that over-approximate a context-free language with a regular language. Our push-down automata with bounded run-time stack are less expensive to operate and require finite resources.

We provide background on the Condor system, remote execution in the computational Grid environment, and security exploits in Section 2. Section 3 presents our analysis techniques in an algorithmic fashion. Experimental results are found in Section 4 and comparison to previous work in Section 5. Related work can be found in Section 6. We conclude in Section 7 with descriptions of several areas of continuing work.

2. Threats

Remote execution is becoming a common scenario. An important class of remotely executing jobs require a communication path back to the local machine that originated the job; the job sends its critical system calls, such as those for file access or network communication, back to the local machine to execute in the context of the submitting user. This type of remote execution occurs in the Condor distributed scheduling system [26], Globus computational Grid infrastructure [13,14], and Java applets.

The implementation associated with our research takes place in the context of Condor. Condor schedules jobs on hosts both within the originator's organization and on machines belonging to other organizations. In addition to scheduling these remote jobs, Condor checkpoints and migrates the jobs as necessary for reliability and performance reasons. It is possible for a given job to execute, at different times, on several hosts in several different administrative domains.

Condor is a prevalent execution environment, particularly for scientific research. For example, in the year 2000, researchers used Condor to solve a 32-year-old unsolved combinatorial optimization problem called nug30 [2]. Remote jobs ran on 2510 processors across the United States and Italy and outside the administrative control of the program's authors. Furthermore, the network path between each remote process and its originating host included public Internet links. A malicious third party with access to either the execution machines or network links could have manipulated the originating machine, as we now detail.

Remote system calls in Condor are simply a variant of a remote procedure call (RPC). A client stub library is linked with the application program instead of the standard system call library. The stub functions within this library package the parameters to the call into a message, send the message over the network to the submitting machine, and await any result. A local agent on the submitting machine services such calls, unpacking the request, executing the call, and packaging and sending any result back to the remote machine.

This RPC model exposes the submitting machine to several vulnerabilities. These vulnerabilities have the common characteristic that a malicious entity on the remote machine can control the job, and therefore control its remote system call stream. This malicious system call stream could cause a variety of bad things to be done to the submitting user. The simplest case of a malicious remote host is when the host's owner (with administrative privileges) takes control of the remote job. More complex and harder-to-track cases might be caused by previous malicious remote jobs. A previously discovered vulnerability in Condor had this characteristic [27]. When a remote job executes, it is typically run as a common, low privilege user, such as "nobody." A malicious user could submit a job that forks (creates a new process) and then terminates. The child process remains running, but it appears to Condor as if the job has terminated. When a new job is scheduled to run on that host, the lurking process detects the newly arrived job and dynamically attaches to the job and takes control of it. The lurker can then generate malicious remote calls that will be executed to the detriment of the machine that originated the innocent job (see Figure 2).

Similar results are possible with less unusual attacks. If the call stream crosses any network that is not secure, a machine on the network may impersonate the application process, generating spoofed calls that may be treated by the local host as genuine. Imposter applets have successfully used impersonation attacks against the servers with whom the original applets communicate [16].

3. Generating Models Using Static Analysis

We start with the binary program that is submitted for execution. Before execution, we analyze the program to produce two components: a checking agent and a modified application (see Figure 3). The checking agent is a local agent that incorporates the model of the application. As the agent receives remote system calls for execution, it first verifies the authenticity of each call by operating the model. Execution continues only while the model remains in a valid state. The modified application is the original program with its binary code rewritten to improve model precision while also offering a modicum of obfuscation. The modified application executes remotely, transmitting its remote system calls to the checking agent.

Our various models are finite-state machines: non-deterministic finite automata (NFA) and push-down automata (PDA). Each edge of an automaton is labeled with an alphabet symbol-here the identity of a remote system call. The automaton has final states, or states where operation of the automaton may successfully cease. The ordered sequences of symbols on all connected sequences of edges from the entry state to a final state define the language accepted by the automaton. For a given application, the language defined by a perfect model of the application is precisely all possible sequences of remote system calls that could be generated by the program in correct execution with an arbitrary input.

Construction of the automaton modeling the application progresses in three stages:

1. A control flow graph (CFG) is built for each procedure in the binary. Each CFG represents all possible execution paths in a procedure.
2. We convert the collection of CFGs into a collection of local automata. Each local automaton models the possible streams of remote system calls generated in a single procedure.
3. We compose these automata at points of function calls internal to the application, producing an interprocedural automaton modeling the application as a whole.

Figure 4(a) shows an example C language program that writes a string to the standard output. The main function translates to the SPARC code in Figure 4(b) when compiled. We include the C code solely for the reader's ease; the remainder of this section demonstrates analysis of the binary code that a compiler and assembler produces from this source program.

3.1. From Binary Code to CFGs

We use a standard tool to read binary code and generate CFGs. The Executable Editing Library (EEL) provides an abstract interface to parse and edit (rewrite) SPARC binary executables [25]. EEL builds objects representing the binary under analysis, including the CFG for each procedure and a call graph representing the interprocedural calling structure of the program. Nodes of the CFG, or basic blocks, contain linear sequences of instructions and edges between blocks represent control flow; i.e. the possible paths followed at branches. Figure 5 shows the CFG for main from Figure 4.

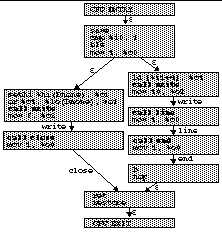Figure 5: Control Flow Graph for main. Control transfers in SPARC code have one delay slot. Outgoing edges of each basic block are labeled with the name of the call in the block.

3.2. From CFGs to Local Automata

For each procedure, we use its CFG to construct an NFA representing all possible sequences of calls the procedure can generate. This is a natural translation of the CFG into an NFA that retains the structure of the CFG and labels the outgoing edges of each basic block with the name of the function call in that block, if such a call exists. Outgoing edges of blocks without a function call are labeled ε. The automaton mirrors the points of control flow divergence and convergence in the CFG and the possible streams of calls that may arise when traversing such flow paths.

Formally, we convert each control flow graph 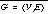into an NFA given by 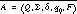, Q being the set of states, Σ the input alphabet, δ the transition relation, q0 the unique entry state, and F the set of accepting states; where:

To reduce space requirements, each NFA is ε-reduced and minimized. The classical ε-reduction algorithm simultaneously determinizes the automaton, an exponential process [19]. We develop a linear time ε-reduction algorithm, shown below, that does not determinize the automaton. The algorithm recognizes that a set of states in a strongly connected component made of ε-edges are reachable from one another without consuming an input symbol and collapses them to a single state.

The resultant graph is the reduced automaton (Figure 6). Using standard algorithms and data structures, our ε-reduction procedure runs in linear time.

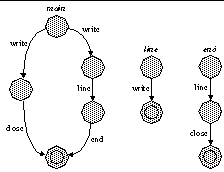Figure 6: Local Automata. The local automata for each of the three functions given in Figure 4 after ε-reduction.

Automaton minimization recognizes equivalent states, where equivalence indicates that all sequences of symbols accepted following the states are identical. Such states are collapsed together, reducing the overall size and complexity of the automaton. An O(n log n) algorithm exists to minimize deterministic automata [18], but it is not easily abstracted to an NFA. Our prototype uses an O(n2) version of the algorithm suitable for an NFA.

3.3. From Local Automata to an Interprocedural Automaton

Constructing an Interprocedural NFA. We extend the notion of a single procedure NFA model to a model of the entire application. The local automata are composed to form one global NFA by call site replacement. We replace every edge representing a procedure call with control flow through the automaton modeling the callee, a common technique used elsewhere to construct system dependence graphs [20] and also used by Wagner and Dean in their work [36,37].

Where there was an edge representing a called function, control now flows through the model of that function. Recursion is handled just as any other function call. Call site replacement reintroduces ε-edges, so the automaton is reduced as before. Figure 7 presents the final automaton, without ε-reduction for clarity.

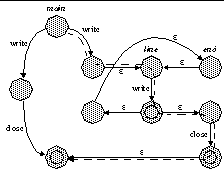Figure 7: Final NFA Model. The automaton produced following call site replacement. ε-reduction has not been performed. The dotted line represents a path not present in the original program but accepted by the model.

There is no replication of automata. Call site replacement links multiple call sites to the same procedure to the same local automaton. Every final state of the called automaton has ε-edges returning to all call sites. Impossible paths exist: control flow may enter the automaton from one call site but return on an ε-edge to another (Figure 7). Such behavior is impossible in actual program execution, but a malicious user manipulating the executing program may use such edges in the model as an exploit. In applications with thousands of procedures and thousands more call sites, such imprecision must be addressed.

Constructing an Interprocedural PDA. Introduction of impossible paths is a classical program analysis problem arising from context insensitive analysis (see e.g. [28]). A push-down automaton eliminates impossible paths by additionally modeling the state of the application's run-time stack. An executing application cannot follow an impossible path because the return site location is stored on its run-time stack. A PDA is context sensitive, including a model of the stack to precisely mirror the state of the running application.

This is an interprocedural change. We construct local automata as before. The ε-edges added during call site replacement, though, now contain an identifier uniquely specifying each call edge's return state (Figure 8). Each ε-edge linking the source of a function call edge to the entry state of the called automaton pushes the return state identifier onto the PDA stack, just as the executing program pushes the return address onto the run-time stack. The ε-edges returning control flow from the callee pop the identifier from the PDA stack, mirroring the application's pop of the return address from its run-time stack. Such a pop edge is traversed only when the identifier on the edge matches the symbol at the top of the stack. The identifiers on the ε-edges define matched sets of edges. Only return edges that correspond to a particular entry edge may be traversed when exiting the called automaton. Since a PDA tracks this calling context, impossible paths cannot exist.

We link local automata using modified call site replacement:

Formally, let the interprocedural PDA be 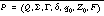, where Q is the set of states, Σ is the input alphabet, Γ is the stack alphabet, δ is the transition relation, q0 is the unique entry state, Z0 is the initial stack configuration, and F is the set of accepting states. Given local NFA models 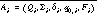for the procedures, the PDA P for the program is given by:

The initially executed automaton, here denoted by A0, is that modeling the function to which the operating system first transfers control, e.g. _start or main.

Unfortunately, a PDA is not a viable model in an operational setting. In a straightforward operation of the automaton, the run-time stack may grow until it consumes all system resources. In particular, the stack size is infinite in the presence of left recursion. To counter left recursion challenges, Wagner and Dean operate the PDA with an algorithm similar to the post* algorithm used in the context of model checking of push-down systems [10]. They demonstrate the algorithm to be prohibitively expensive [36,37]. Addressing imprecision requires a more reasonable approach.

3.4. Optimizations to Address Sources of Imprecision

Imprecisions in the models arise from impossible paths, context insensitive analysis, and malicious argument manipulation. We develop several optimizations that target these particular sources of imprecision while maintaining efficiency.

3.4.1. Impossible Paths

Discarding push-down automata as not viable requires impossible paths to be readdressed. Impossible paths arise at the final states of automata that are spliced into multiple call sites. The ε-return edges introduce divergent control flow where no such divergence exists in the application. We have developed several NFA model optimizations to reduce the effect of return edges upon the paths in the model.

Dead Automata Removal. A leaf automaton is a local automaton that contains no function call edges. Any leaf automaton that contains no remote system call edges is dead-it models no control flow of interest. Any other local automaton that contains a call edge to the dead leaf may replace that call edge with an ε-edge. This continues, recursively, backward up the call chain. To eliminate impossible paths introduced by linking to a dead automaton, we insert this dependency calculation step prior to call site replacement.

Automata Inlining. Recall that in call site replacement, all calls to the same function are linked to the same local automaton. Borrowing a suitable phrase from compilers, we use automata inlining to replace each call site with a splice to a unique copy of the called automaton. Impossible paths are removed from this call site at the expense of a larger global automaton. In theory, the global automaton may actually be smaller and less dense because false edges introduced by impossible paths will not be present, however we have generally found that the state space of the automaton does increase significantly in practice.

Single-Edge Replacement. An inlining special case, single-edge replacement is a lightweight inlining technique used when the called automaton has exactly one edge. The function call edge is simply replaced with a copy of the edge in the callee. This is inexpensive inlining, for no states nor ε-edges are added, yet the model realizes inlining gains.

Bounded Stack Model. Revisiting the idea of a PDA model, we find that both the problems of infinite left recursion and, more generally, unbounded stacks may be solved simply by limiting the maximum size of the run-time stack. For some N, we model only the top N elements of the stack; all pop edges are traversed when the stack becomes empty. The state space of the run-time automaton is now finite, requiring only finite memory resources. Correspondingly, the language accepted by the bounded-stack PDA is regular, but more closely approximates a context-free language than a regular NFA.

Unfortunately, a bounded stack introduces a new problem at points of left recursion. Any recursion deeper than the maximum height of the stack destroys all context sensitivity: the stack first fills with only the recursive symbol; then, unwinding recursion clears the stack. All stack symbols prior to entering recursion are lost.

Hybrid Model. This recursion effect seems to be the opposite of what is desired. For many programs, recursion typically involves a minority of its functions. We consider that it may be more precise to discard recursive symbols rather than symbols prior to entering recursion. Our hybrid model uses both NFA and PDA edges during interprocedural construction to accomplish this. Call site replacement uses simple ε-edges when the procedure call is on a recursive cycle. A stack symbol is used only when a call is not recursive. Recursion then adds no symbols to the PDA stack, leaving the previous context sensitivity intact. As in the bounded-stack PDA, the hybrid automaton defines a regular language that over-approximates the context-free grammar accepted by a true PDA.

3.4.2. Context Insensitivity

Regardless of the technique used to construct the interprocedural model, the analysis basis for all local models is context insensitive. We take all control flow paths as equally likely irrespective of the previous execution flow and do not evaluate predicates at points of divergence. This straightforward analysis leads to a degree of non-determinism in the local automata that we seek to reduce. Reducing non-determinism decreases the size of the frontier of possible current states in the automaton at run-time. There are, in turn, fewer outgoing edges from the frontier, improving efficiency and precision.

Renaming. During program analysis, every remote call site is assigned a randomly generated name. We produce a stub function with this random name that behaves as the original call and rewrite the binary program so that the randomly named function is called. That is, rather than calling a remote system call stub named, say, write, the call is to a stub named _3998. We are essentially passing all call site names through a one-time encryption function. The key is stored at the checking agent (on the submitting machine), which translates the random name back to the original call name before execution.

All call sites are thus differentiated. Two separate calls to the same function now appear as calls to different functions. The random names label edges in the automaton and serve as the input symbol at model run-time. Renaming reduces non-determinism, for the model knows precisely where the program is in execution after every received call. Comparing Figure 9 with Figure 6, we see that the automaton for main becomes fully deterministic with renamed call sites.

This is an alphabet change, moving from symbols indicating call names to the potentially larger set of symbols defining individual call sites. An attacker must specify attacks given this randomly generated alphabet, thus requiring analysis to recover the transformations. Further, only remote calls that are actually used in the program may be used in an attack. Renamed calls are generated from call sites, blocking from use any unused remote call stub still linked into the application.

Call site renaming produces equivalent but less human-readable program text, acting as a simplistic obfuscation technique [8]. The checking agent maintains the transformations; recovery by a malicious individual requires program analysis to indicate likely remote call names given the context of the call in the program. Since we can rewrite the binary code, further obfuscation techniques are applicable: arguments may be reordered and mixed with dummy arguments on a per-call-site basis, for example. More general methods to obscure control flow are similarly possible, although we have not pursued such techniques.

A recent paper by Barak et. al. presents a complexity-theoretic argument that proves the impossibility of a specific class of obfuscating transformations [5]. They define an obfuscated program as a "virtual black box", i.e., any property that can be computed by analyzing the obfuscated program can also be computed from the input-output behavior of the program. In contrast to their work, we require that it is computationally hard for an adversary to recover the original system calls corresponding to the renamed calls, i.e., it is computationally hard for the adversary to invert the renaming function. Hence, our obfuscation requirement is much weaker than the "virtual blackbox" requirement imposed by Barak et. al. However, we are not claiming theoretical guarantees of the strength of our obfuscation transformation but merely observing that the theoretical results presented by Barak et. al. do not directly apply in our context.

Null calls. Insertion of null calls-dummy remote system calls that translate to null operations at the checking agent-provides similar effects. We place the calls within the application so that each provides execution context to the checking agent, again reducing non-determinism.

For example, null calls may be placed immediately following each call site of a frequently called function. Recall that we introduce impossible paths during call site replacement, and specifically where we link the final states of a local automaton to the function call return states. Inserting the null calls at the function call return sites distinguishes the return locations. Only the true return path will be followed because only the symbol corresponding to the null call at the true return site will be transmitted. The other impossible paths exiting from the called automaton are broken.

There is a run-time element to renaming and null call insertion. While reducing non-determinism, the possible paths through the automaton remain unchanged (although they are labeled differently). To an attacker with knowledge of the transformations, the available attacks in a transformed automaton are equivalent to those in the original, provided the attacker takes control of the call stream before any remote calls occur. An attacker who assumes control after one or more remote calls will be restricted because operation of the model to that point will have been more precise.

3.4.3. Argument Manipulation

A remote system call exists within a calling context that influences the degree of manipulation available to a malicious process. For example, at a call site to open, a malicious process could alter the name of the file passed as the first argument to the call. A model that checks only the names of calls in the call stream would accept the open call as valid even though it has been maliciously altered. The context of the open call, however, may present additional evidence to the checking agent that enables such argument modifications to be detected or prevented.

Argument Recovery. As local automata are constructed, we recover all statically determined arguments by backward slicing on the SPARC argument registers. In backward register slicing, we iterate through the previous instructions that affect a given register value [34]. Essentially, we are finding the instructions that comprise an expression tree. We simulate the instructions in software to recover the result, used here as an argument to a call. We successfully recover numeric arguments known statically and strings resident in the data space of the application. The checking agent stores all recovered arguments so that they are unavailable for manipulation.

In Figure 10, the backward slice of register %o1 at the point of the second call to write in function main iterates through the two instructions that affect the value of %o1. Only the emphasized instructions are inspected; instructions that do not affect the value %o1 are ignored. In this case, Dnone is a static memory location indicating where in the data space the string for "none\n" resides. We recover the string by first simulating the instructions sethi and or in software to compute the memory address and then reading the string from the data space.

A similar analysis is used to determine possible targets of indirect calls. Every indirect call site is linked to every function in the program that has its address taken. We identify such functions by slicing backward on the register written at every program point to determine if the value written is an entry address. Our register slicing is intraprocedural, making this a reasonable computation.

3.5. Unresolved Issues

Dynamic Linking. A dynamically linked application loads shared object code available on the remote machine into its own address space. Although this code is non-local, we can fairly assume that the remote machine provides standard libraries to ensure correct execution of remote jobs. Analysis of the local standard libraries would then provide accurate models of dynamically linked functions.

Although straightforward, we have not yet implemented support for dynamically linked applications. Some libraries on Solaris 8, such as libnsl.so, use indirect calls extensively. As we improve our handling of indirect calls, we expect to handle these applications.

Signal Handling. During execution, receipt of a signal will cause control flow to jump in and out of a signal handler regardless of the previous execution state. This entry and exit is undetectable to the checking agent save the alarms it may generate. As we already instrument the binary, we expect to insert null calls at the entry and exit points of all signal handlers to act as out-of-band notifications of signal handler activity. These instrumentations have not yet been implemented.

Multithreading. Both kernel and user level thread swaps are invisible to the checking agent; thread swaps will likely cause the run-time model to fail, and this remains an area for future research. User level thread scheduling would allow instrumentation of the scheduling routines so that the checking agent could swap to the corresponding model for the thread. A kernel scheduling monitor would require kernel modifications and is currently not under consideration.

Interpreted Languages. Programs written in languages such as SML [3] and Java are compiled into an intermediate form rather than to native binary code. To execute the program, a native-code run-time interpreter reads this intermediate representation as data and executes specific binary code segments based upon this input. Binary code analysis will build a model of the interpreter that accepts all sequences of remote calls that could be generated by any compiled program. A precise model for a specific application can be built either with knowledge of the intermediate representation and the way it is interpreted by the run-time component or by partial evaluation of the interpreter [21]. However, if the program is compiled into native code before execution, as is common in many Java virtual machine implementations [33], our techniques could again be used to construct program-specific models of execution.

4. Experimental Results

We evaluate our techniques using two criteria: precision and efficiency. A precise model is one that incorporates all sequences of calls that may be generated by an application but few or no sequences that cannot. An efficient model is one that adds only a small run-time overhead. Only efficient models will be deployed, and only precise models are of security interest.

This section looks first at a prototype tool we used to evaluate our techniques and models. We examine metrics that measure precision and propose a method to identify unsafe states in an automaton. Our tests show that although null call insertion markedly improves the precision of our models, care must be used so that the additional calls do not overwhelm the network. We finally examine optimizations, including renaming, argument recovery, and stack abstractions that improve the quality of our models.

4.1. Experimental Setup

We implemented an analyzer and a run-time monitor for a simulated remote execution environment to test the precision and efficiency of our automaton models. The analyzer examines the submitted binary program and outputs an automaton and a modified binary. The automaton is read and operated by a stand-alone process, the monitor, that acts as the checking local agent, communicating with the modified program using message-passing inter-process communication. The monitor is not an RPC server and only verifies that the system call encountered by the program is accepted by the model. If the monitor successfully updates the automaton, the original system call proceeds in the rewritten application.

Our analyzer and simulated execution environment run on a Sun Ultra 10 440 Mhz workstation with 640 Mb of RAM running Solaris 8. To simulate a wide-area network, we add a delay per received remote system call equivalent to the round trip time between a computer in Madison, Wisconsin and a computer in Bologna, Italy (127 ms). We do not include a delay for data transfer, for we do not statically know what volume of data will be transferred. Null calls require no reply, so the delay added per null call is the average time to call send with a 20 byte buffer argument (13 μs). During evaluation, the collection of Solaris libc kernel trap wrapper functions defines our set of remote system calls.

We present the analysis results for six test programs (see Table 1 for program descriptions and workloads and Table 2 for statistics). All workloads used default program options; we specified no command line switches.

As we have not implemented general support for dynamically linked functions, we statically link all programs. However, several network libraries, such as libresolv.so, can only be dynamically linked on Solaris machines. We analyze these libraries using the same techniques as for an application program, but store the generated automata for later use. When our analysis of a program such as procmail or finger reveals a call to a dynamically linked function, we read in the stored local automaton and continue. We currently ignore the indirect calls in dynamically linked library functions unless the monitor generates an error at run-time at the indirect call location.

4.2. Metrics to Measure Precision and Efficiency

We wish to analyze both the precision of our models and the efficiency with which the monitor may operate them. Precision dictates the degree to which an adversary is limited in their attacks, and thus the usefulness of the model as a counter-measure. Efficient operation is a requirement for deployment in real remote execution environments.

For comparison, we measure automaton precision using Wagner and Dean's dynamic average branching factor metric [36,37]. This metric first partitions the system calls into two sets, dangerous and safe. Then, during application execution and model operation, the number of dangerous calls that would next be accepted by the model is counted following each operation. The total count is averaged over the number of operations on the model. Smaller numbers are favorable and indicate that an adversary has a small opportunity for exploit.

Our efficiency measurements are straightforward. Using the UNIX utility time, we measure each application's execution time in the simulated environment without operating any model. This is a baseline measure indicating delay due to simulated network transit overhead, equivalent to a remote execution environment's run-time conditions. We then turn on checking and various optimizations to measure the overhead introduced by our checking agent. We find the NFA model efficient to operate but the bounded PDA disappointingly slow. However, the extra precision gained from inclusion of null calls into the bounded PDA model dramatically improves efficiency.

4.3. The NFA Model

We evaluate the models of the six test programs with respect to precision and efficiency. Our baseline analyzer includes renaming, argument recovery, dead automaton removal, and single-edge replacement. Using the NFA model, we compare the results of several null call placement strategies against this baseline and consider the trade-off between performance and efficiency due to the null call insertion.

We use four different null call placement strategies. First, no calls are inserted. Second, calls are inserted at the entry point of every function with a fan-in of 10 or more-that is, the functions called by 10 or more other functions in the application. Third, we insert calls at the entry point of every function with a fan-in of 5 or greater. Fourth, we instrument functions with a fan-in of 2 or more. We have tried three other placement strategies but found they occasionally introduced a glut of null calls that would overwhelm the network: adding calls to all functions on recursive cycles; to all functions whose modeling automaton's entry state is also a final state, ensuring every call chain generates at least one symbol; and to functions with fan-in of 1 or more. As we expected, this sequence of greater instrumentation increases the precision and quality of the automata while negatively impacting performance as the extra calls require additional network activity. More generally, the problem of selecting good null call insertion points is similar to that of selecting optimal locations to insert functions for program tracing, a topic of previous research [4]. We will investigate the use of such selection algorithms for our future implementations.

We found that null call insertion dramatically improved precision. Figure 11 shows the dynamic average branching factor for the six test programs at each of the null call placement strategies. Instrumenting at the maximum level improves precision over non-instrumented models by an order of magnitude or more. Even though null call insertion adds edges to the local automata, we observe that the number of edges in the final automaton are usually significantly lower, indicating that call site replacement introduces fewer impossible paths. The edge count in procmail's model drops by an order of magnitude even though the state count increases modestly. We believe these results demonstrate the great potential of introducing null calls.

Although unfortunate, null call insertion has the expected detrimental effect on application run-times. Each null call encountered during execution drops another call onto the network for relay to the checking agent. The application need not wait for a response, but each call is still an expensive kernel trap and adds to network traffic. Table 3 shows the additional execution time resulting from operation of models with null calls. Table 4 lists the bandwidth requirements of each insertion level for null calls that each consume 100 bytes of bandwidth.

We make two primary observations from these results. First, our NFA model is incredibly efficient to operate at run-time when no null calls have been inserted. Second, inserting null calls in functions with fan-in 5 or greater is a good balance between precision gain and additional overhead in our six test programs. Unfortunately, two programs require moderate bandwith at this instrumentation level. We believe the varying bandwidth needs among our test programs are due in part to our naive null call insertion strategies. We expect that an algorithm such as that developed by Ball and Larus [4] will reduce bandwidth requirements and improve consistency among a collection of programs.

4.4. Effects of Optimizations

We analyzed procmail further to evaluate renaming, argument recovery, and our stack abstractions. We did not analyze automaton inlining here, for it surprisingly proved to be an inefficient optimization. Inlining added significant overhead to model construction but delivered little gain in precision. Similarly, we found the run-time characteristics of the hybrid model to be nearly identical to those of the bounded PDA. We will not examine inlining or the hybrid model in any greater detail.

To see the effects of renaming and argument recovery, we selectively turned off these optimizations. The graph in Figure 12 measures average branching factor dependent on use of call site renaming and of argument recovery in the program procmail. As we expected, both renaming and argument recovery reduced the imprecision in the model. The reduction produced by renaming is solely due to the reduction in non-determinism. Argument recovery reduces imprecision by removing arguments from manipulation by an adversary. Renaming and argument recovery together reduce imprecision more than either optimization alone.

At first glance, it may seem counter-intuitive that argument recovery should reduce imprecision to a greater degree than renaming. Argument recovery is, after all, a subset of renaming; static arguments distinguish the call site. However, an attacker cannot manipulate a recovered argument, so system calls that were dangerous with unknown arguments become of no threat with argument recovery.

We analyzed the bounded PDA model for procmail with stack bounds from 0 to 10. Figure 13 shows the average branching factors of our PDA at varying levels of null call instrumentation and bounded stack depth. Figures 14 and 15 show the run-time overheads of these models at two different time scales.

Null call insertion has a surprising effect on operation of the bounded stack models. The added precision of the null calls actually decreases run-time overheads. We were surprised to discover cases where the bounded-stack PDA with null call instrumentation was nearly as efficient to operate as an NFA model, but at a higher level of precision. Observe that higher levels of null call instrumentation actually reduce the execution times, as operation of the models becomes more precise.

Increasing the stack size produces a similar effect. The plots for instrumentation in functions with fan-in of 5 in Figure 14 and in functions with fan-in of 10 in Figure 15 show a common pattern. Up until a stack bound of size 6, the model's efficiency improves. More execution context is retained, so fewer paths in the model are possible. As the state grows past a bound of 6, the cost of increased state begins to dominate. Finding this transition value is an important area for future research.

4.5. Discussion on Metrics

Measuring precision with the dynamic average branching factor metric ignores several important considerations:

1. An attack likely consists of a sequence of system calls and is not a single call in isolation. A call may be dangerous only when combined with other calls.
2. The attacker could steer execution through one or more "safe" system calls to reach a portion of the model that accepts an attack sequence. Perhaps a typical run of the program does not reach this area of the model, so the dangerous edges do not appear in the dynamic average branching factor. Such safe edges should not cover the potential for an attack downstream in the remote call sequence.

We do not see any obvious dynamic metric that easily overcomes these objections. The straightforward static analogue to dynamic average branching factor is static average branching factor, the same count averaged over the entire automaton with all states weighted equally. The prior complaints remain unsatisfied.

We propose a metric that combines static and dynamic measurements. Our average adversarial opportunity metric requires two stages of computation: first, the automaton modeling the application is composed with a set of attack automata to identify all model states with attack potential; then, the monitor maintains a count of the dangerous states encountered during run-time. "Attack potential" indicates a known attack is possible beginning at the current state or at a state reachable from it. We are locating those positions in the model where an adversary could successfully insert an attack and counting visits to those states at run-time.

5. Comparison with Existing Work

We measured dynamic average branching factor and execution overhead for comparison with the earlier work of Wagner and Dean. We compare only the NFA model, as it is the only model our work has in common with their own. They analyzed four programs; two of them, procmail and finger intersect our own experimental set. Although we do not know what version of finger Wagner and Dean used, we compared their numbers against our analysis of GNU finger. We used call site renaming, argument recovery, and single-edge replacement. The results for Wagner and Dean include argument recovery. (They have no analogue to renaming or edge replacement). On the two programs, we observed a significant discrepancy between their reported precision values and those we could generate. Upon investigation, it appears to be caused by the differences in library code between our respective test platforms. Wagner and Dean analyzed programs compiled on Red Hat Linux, but we use Solaris 8. Solaris is an older operating system and includes more extensive library code in its standard libraries. Solaris libc, for example, is structured differently than glibc on Linux and includes functionality not found in glibc. To see the differences, compare Figure 17, the automaton for the socket system call in glibc, with Figure 16, the automaton for the same function in Solaris libc. In this case, the Solaris socket function includes code maintaining backwards compatibility with an earlier method of resolving the device path for a networking protocol. While socket has the greatest difference of the functions we have inspected, we have found numerous other library functions with a similar characteristic. Simply, Linux and Solaris have different library code and we have found the Solaris code to be the more complex.

To better understand the influence of this different library code base, we identified several functions in Solaris libc that differed significantly from the equivalent function in glibc. We instrumented the code of the identified functions so that each generates a remote system call event in a manner similar to glibc. As we expected, the average branching factor of each model dropped significantly (Figure 18). Because we intentionally instrument the library functions incorrectly, the model generated is semantically invalid. However, we believe the change in precision values reinforces our hypothesis.

Our model operation improves significantly over the work of Wagner and Dean. Figure 18 also shows overheads in each of the two programs attributed to model operation. Our gain is partly due to implementation: Wagner and Dean wrote their monitor in Java. Our code runs natively and is highly efficient, introducing only negligible delay.

6. Related Work

There are three areas with techniques and goals similar to those considered in this paper: applications of static analysis to intrusion detection, statistical anomaly-detection-based intrusion detection, and secure agentry. We compare the techniques presented in this paper with the existing research in the three areas.

Our work applies and extends the techniques described by Wagner and Dean [36,37]. To our knowledge, they were the first to propose the use of static analysis for intrusion detection. However, they analyzed C source code by modifying a compiler and linker to construct application models. Our analysis is performed on binaries, independent of any source language or compiler, removing the user's burden to supply their source code. We also propose several optimizations and program transformations that improve model precision and efficiency. We believe the optimizations proposed in this paper are important contributions and can be used by other researchers working in this area.

There is a vast body of work applying dynamic analysis to intrusion detection. In statistical anomaly-detection-based intrusion detection systems such as IDES [9], a statistical model of normal behavior is constructed from a collection of dynamic traces of the program. For example, a sequence of system calls, such as that produced by the utilities strace and truss, can be used to generate a statistical model of the program (see Forrest et al. [12]). Behaviors that deviate from the statistical model are flagged as anomalous but are not a guarantee of manipulation. Theoretically, we can use a statistical program model in our checking agent. Practically, however, these models suffer from false alarm rates; i.e. they reject sequences of system calls that represent acceptable but infrequent program behavior. Human inspection of jobs flagged as anomalous is inappropriate in our setting so we did not pursue this approach.

The literature on safe execution of mobile agents on malicious hosts (also known as secure agentry) is vast. The reader is referred to the excellent summary on various techniques in the area of secure agentry by Schneider [31]. We are currently exploring whether techniques from this area, such as replication, are useful in our setting.

7. Future Work

We continue progressing on a number of fronts. Foremost, we are working to expand our infrastructure base of static analysis techniques to include points-to analysis for binaries and regular expression construction for arguments. Standard points-to analysis algorithms are designed for a higher-level source language and often rely on datatype properties evident from the syntax of the code. We will adapt the algorithms to the weakly-typed SPARC code. For arguments, we envision using stronger slicing techniques to build regular expressions for arguments not statically determined. Better code analyses will produce more precise models.

We have two research areas targeting run-time overhead reductions in our complex models. To reduce the impact of null call insertions, we will investigate adaptations of the Ball and Larus algorithm to identify optimal code instrumentation points for minimum-cost code profiling [4]. To reduce the overhead of our PDA models, we will collapse all run-time values at the same automaton state into a single value with a DAG representing all stack configurations. When traversing outgoing edges, a single update to the DAG is equivalent to an individual update to each previous stack. Our hope is to make our complex and precise models attractive for real environments.

We will add general support for dynamically linked applications and signal handlers to our analysis engine, enabling analysis of larger test programs.

To better measure the attack opportunities afforded by our models, we will implement the average adversarial opportunity metric and create a collection of attack automata. Having an accurate measure of the danger inherent in an automaton better enables us to develop strategies to mitigate the possible harm.

Acknowledgments

We thank David Wagner for patiently answering questions about his work and for providing his specification of dangerous system calls. David Melski pointed out the relevance of the Ball and Larus research [4]. We had many insightful discussions with Tom Reps regarding static analysis. Hong Lin initially researched solutions to the remote code manipulation vulnerability. Glenn Ammons provided helpful support for EEL. We thank the other members of the WiSA security group at Wisconsin for their valuable feedback and suggestions. Lastly, we thank the anonymous referees for their useful comments.

Availability

Our research tool remains in development and we are not distributing it at this time. Contact Jonathon Giffin, giffin@cs.wisc.edu, for updates to this status.

References

1. A.D. Alexandrov, M. Ibel, K.E. Schauser, and C.J. Scheiman, "SuperWeb: Towards a Global Web-Based Parallel Computing Infrastructure", 11th IEEE International Parallel Processing Symposium, Geneva, Switzerland, April 1997.
2. K. Anstreicher, N. Brixius, J.-P. Goux, and J. Linderoth, "Solving Large Quadratic Assignment Problems on Computational Grids", 17th International Symposium on Mathematical Programming, Atlanta, Georgia, August 2000.
3. A.W. Appel and D.B. MacQueen, "Standard ML of New Jersey", Third International Symposium on Programming Language Implementation and Logic Programming, Passau, Germany, August 1991. Also appears in J. Maluszynski and M. Wirsing, eds., Programming Language Implementation and Logic Programming, Lecture Notes in Computer Science #528, pp. 1-13, Springer-Verlag, New York (1991).
4. T. Ball and J.R. Larus, "Optimally Profiling and Tracing Programs", ACM Transactions on Programming Languages and Systems 16, 3, pp. 1319-1360, July 1994.
5. B. Barak, O. Goldreich, R. Impagaliazzo, S. Rudich, A. Sahai, S. Vadhan, and K. Yang, "On the (Im)possibility of Obfuscating Programs", 21st Annual International Cryptography Conference, Santa Barbara, California, August 2001. Also appears in J. Kilian, ed., Advances in Cryptology - CRYPTO 2001, Lecture Notes in Computer Science #2139, pp. 1-18, Springer-Verlag, New York (2001).
6. E. Belani, A. Vahdat, T. Anderson, and M. Dahlin, "The CRISIS Wide Area Security Architecture", Seventh USENIX Security Symposium, San Antonio, Texas, January 1998.
7. S. Chow, Y. Gu, H. Johnson, and V.A. Zakharov, "An Approach to the Obfuscation of Control-Flow of Sequential Computer Programs", Information Security Conference `01, Malaga, Spain, October 2001.
8. C. Collberg, C. Thomborson, and D. Low, "Breaking Abstractions and Unstructuring Data Structures", IEEE International Conference on Computer Languages, Chicago, Illinois, May 1998.
9. D.E. Denning and P.J. Neumann, Requirements and Model for IDES-A Real-Time Intrusion Detection System, Technical Report, SRI International, August 1985.
10. J. Esparza, D. Hansel, P. Rossmanith, and S. Schwoon, "Efficient Algorithms for Model Checking Pushdown Systems", 12th Conference on Computer Aided Verification, Chicago, Illinois, July 2000. Also appears in E.A. Emerson and A.P. Sistla, eds., Computer Aided Verification, Lecture Notes in Computer Science #1855, pp. 232-247, Springer-Verlag, New York (2000).
11. G.E. Fagg, K. Moore, and J.J. Dongarra, "Scalable Networked Information Processing Environment (SNIPE)", Supercomputing `97, San Jose, California, November 1997.
12. S. Forrest, S.A. Hofmeyr, A. Somayaji, and T.A. Longstaff, "A Sense of Self for Unix Processes", 1996 IEEE Symposium on Research in Security and Privacy, Oakland, California, May 1996.
13. I. Foster and C. Kesselman, "Globus: A Metacomputing Infrastructure Toolkit", The International Journal of Supercomputer Applications and High Performance Computing 11, 2, pp. 115-129, Summer 1997.
14. I. Foster and C. Kesselman, eds., The Grid: Blueprint for a New Computing Infrastructure, Morgan Kaufmann, San Francisco (1998).
15. A.K. Ghosh, A. Schwartzbard, and M. Schatz, "Learning Program Behavior Profiles for Intrusion Detection", 1st USENIX Workshop on Intrusion Detection and Network Monitoring, Santa Clara, California, April 1999.
16. J.T. Giffin and H. Lin, "Exploiting Trusted Applet-Server Communication", Unpublished Manuscript, 2001. Available at http://www.cs.wisc.edu/~giffin/.
17. F. Hohl, "A Model of Attacks of Malicious Hosts Against Mobile Agents", 4th ECOOP Workshop on Mobile Object Systems: Secure Internet Computations, Brussels, Belgium, July 1998.
18. J. Hopcroft, An n log n Algorithm for Minimizing States in a Finite Automaton, Theory of Machines and Computations, pp. 189-196, Academic Press, New York (1971).
19. J.E. Hopcroft, R. Motwani, and J.D. Ullman, Introduction to Automata Theory, Languages, and Computation, Addison Wesley, Boston (2001).
20. S. Horwitz and T. Reps, "The Use of Program Dependence Graphs in Software Engineering", 14th International Conference on Software Engineering, Melbourne, Australia, May 1992.
21. N.D. Jones, C.K. Gomard, and P. Sestoft, Partial Evaluation and Automatic Program Generation, Prentice Hall International Series in Computer Science, Prentice Hall, Englewood Cliffs, New Jersey (1993).
22. C. Ko, G. Fink, and K. Levitt, "Automated Detection of Vulnerabilities in Privileged Programs by Execution Monitoring", 10th Annual Computer Security Applications Conference, Orlando, Florida, 1994.
23. C. Ko, "Logic Induction of Valid Behavior Specifications for Intrusion Detection", 2000 IEEE Symposium on Security and Privacy, Oakland, California, 2000.
24. L. Lamport, R. Shostak, and M. Pease, "The Byzantine Generals Problem", ACM Transactions on Programming Languages and Systems 4, 3, pp. 382-401, July 1982.
25. J.R. Larus and E. Schnarr, "EEL: Machine-Independent Executable Editing", SIGPLAN `95 Conference on Programming Language Design and Implementation, La Jolla, California, June 1995.
26. M. Litzkow, M. Livny, and M. Mutka, "Condor-A Hunter of Idle Workstations", 8th International Conference on Distributed Computer Systems, San Jose, California, June 1988.
27. B.P. Miller, M. Christodorescu, R. Iverson, T. Kosar, A. Mirgorodskii, and F. Popovici, "Playing Inside the Black Box: Using Dynamic Instrumentation to Create Security Holes", Parallel Processing Letters 11, 2/3, pp. 267-280, June/September 2001. Also appears in the Second Los Alamos Computer Science Institute Symposium, Sante Fe, NM (October 2001).
28. T. Reps, "Program Analysis via Graph Reachability", Information and Software Technology 40, 11/12, pp. 701-726, November/December 1998.
29. J.H. Saltzer, "Protection and the Control of Information Sharing in Multics", Communications of the ACM 17, 7, pp. 388-402, July 1974.
30. T. Sander and C.F. Tschudin, "Protecting Mobile Agents Against Malicious Hosts", in G. Vigna, ed., Mobile Agents and Security, Lecture Notes in Computer Science #1419, pp. 44-60, Springer-Verlag, New York (1998).
31. F.B. Schneider, "Towards Fault-tolerant and Secure Agentry", 11th International Workshop on Distributed Algorithms, Saarbrucken, Germany, September 1997.
32. SETI@home: Search for Extraterrestrial Intelligence at Home, 23 January 2002, http://setiathome.ssl.berkeley.edu/.
33. Sun Microsystems, Java Virtual Machines, 11 May 2002, http://java.sun.com/j2se/1.4/docs/guide/vm/.
34. F. Tip, "A Survey of Program Slicing Techniques", Journal of Programming Languages 3, 3, pp.121-189, September 1995.
35. A. Vahdat, T. Anderson, M. Dahlin, E. Belani, D. Culler, P. Eastham, and C. Yoshikawa, "WebOS: Operating System Services for Wide Area Applications", Seventh International Symposium on High Performance Distributed Computing, Chicago, Illinois, July 1998.
36. D.A. Wagner, Static Analysis and Computer Security: New Techniques for Software Assurance, Ph.D. Dissertation, University of California at Berkeley, Fall 2000.
37. D. Wagner and D. Dean, "Intrusion Detection via Static Analysis", 2001 IEEE Symposium on Security and Privacy, Oakland, California, May 2001.
38. C. Wang, J. Davidson, J. Hill, and J. Knight, "Protection of Software-based Survivability Mechanisms", International Conference of Dependable Systems and Networks, Goteborg, Sweden, July 2001.
39. C. Warrender, S. Forrest, and B. Pearlmutter, "Detecting Intrusions Using System Calls: Alternative Data Models", 1999 IEEE Symposium on Security and Privacy, Oakland, California, May 1999.

This work is supported in part by Office of Naval Research grant N00014-01-1-0708, Department of Energy grants DE-FG02-93ER25176 and DE-FG02-01ER25510, Lawrence Livermore National Lab grant B504964, and NSF grant EIA-9870684.

The U.S. Government is authorized to reproduce and distribute reprints for Governmental purposes, notwithstanding any copyright notices affixed thereon.

The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of the above government agencies or the U.S. Government.