Simulating Cloth
Key to the "Gertie, Interrupted" is a simulation of curtains in the window of one of the set pieces.  The following is a description of the Michael's implementation of cloth for this part of the feature.
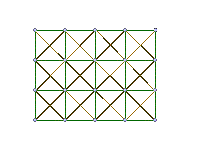
The green vertical and horizontal rows in this image represent springs connecting masses (grey).  The stiffness associated with these green springs relate directly to the stretch in a piece of cloth.  The orange diagonals represent springs connecting diagonally adjacent masses.  The stiffness of these springs relates to the shear of the cloth.

Mass
Cloths have a variety of densities from the heaviest carpet to the lightest silk.  Representing a continuous piece of cloth by a membrane or parametric surface would be beyond the scope of this animation project, so we instead lump the mass of regions of the cloth into point masses and connect them by springs.  These masses will be subject to Newton's laws with forces being applied by springs, gravity, air density, and air pressure.

The mass of each is simply the product of the density and one-fourth the area of the cells surrounding the given mass.  Note: this simplification does not look as bad as it sounds once a cubic surface is fit through the mass locations.

The point masses are represented in the simulation by three arrays of points.  These arrays hold the positions of the masses for the previous, current, and next time steps.

Warp and Weft Threads
The physical effects of the threads in a piece of cloth can be approximated by simulating the forces of springs connecting our point masses in a mesh-like structure as shown on the left.  We simulate the warp and weft threads of the cloth with vertical and horizontal spring forces respectively.  The interaction of the warp and weft threads under loads that would change the orthogonality of these warp and weft is simulated by diagonal spring forces connecting diagonally adjacent masses.

Each spring is assumed to have a nominal length that depends on its orientation in the mesh.  The forces acting between masses are computed by measuring the distance between a subject mass and each of its neighbors.  The difference between this distance and the nominal length of the spring connecting these masses is multiplied by the appropriate spring constant.

This model is still incomplete, we still need a way to simulate the (typically very low) resistance of the threads to bending.
 

 
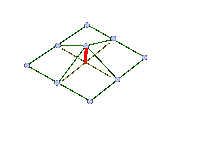This image shows a subset of the cloth system in the neighborhood of one mass (shear springs omitted for clarity.)  The red line represents a pair of springs pulling the center mass toward the average position of the vertically and horizontally adjacent masses.  The stiffness of this spring relates to the bending resistance of the threads in the cloth.
Warp and Weft Threads in Bending
The threads in cloth exhibit a resistance to bending, as evidenced by the rounded appearance of folds in the clothing you wear.  This resistance to bending is simulated by spring forces that attempt to keep the structure of the cloth flat.  Locally, the cloth simulation attempts to maintain the flatness of the structure by applying a flattening force computed by comparing a given mass's position pi,j to the average position of its neighbors; multiplying this by the bending spring constant kbend something like:
fflatten=0.25kbend(pi-1,j+pi+1,j+pi,j-1+pi,j+1-4pi,j)
Even this model is incomplete, since there will be both air resistance to the movement of the cloth, as well as internal damping within the cloth fibers.

Damping
To more accurately simulate real cloth, and promote numerical stability, the friction effects of air and the damping of the spring forces are simulated with a generalized damping force.  This force is proportional, and in a direction opposite, to the velocity of each point mass.

Euler Steps
The action of a spring under a time-varying force is modeled by the following equation:
   (1)
In the simulation, we store only the position information for each mass at the previous two time steps and use this to compute the motion of the mass at the current time step.  The velocity of each mass is approximated by:
   (2)
And the acceleration is approximated by:
   (3)
Substituting (2) and (3) into (1) we get:
where fi is the sum of the forces acting on the subject mass.  Rolling the kxi term into the applied forces, and solving for xi, we get:
By using a sufficiently small time steps, we march the simulation forward, computing new positions for the masses at any future time.  The current implementation uses a time step of 0.001 seconds.

This method of explicitly computing the next state of the masses based on their current state is known as an Euler step. The method is very sensitive to the step size, so we must use small steps resulting in a slow simulation. For our purposes, though, this simple approach is fine- we'll simply output the mass positions at the appropriate time step and allow Maya to interpolate them over time. We justify the extra running time in terms of the savings in projected development and debugging time required to implement cloth using the recommended implicit method.

The Software
We can use a coarse mesh to simulate the behavior of the cloth, and export the result to Maya in the form of a script that creates a cubic spline surface and keyframes the control vertices based on the positions of the point masses.  The result is a very convincing simulation of cloth.
 
Downloading
The software (MS/Windows+OpenGL) and source code is available for download.

Running
The software can be run by simply downloading it to the Windows desktop, or another appropriate location.  After double clicking on the program icon, the program will display a dialog box asking you to specify the size of cloth you would like to simulate.  The default values seem to work reasonably well.  Simply press  to start the simulation.  Note, the software simulates a tabbed curtain with every 8th mass fixed across the top edge.

Controlling the Simulation
The parameters controlling the simulation are accessible by choosing View->Cloth Controls from the menu at the top of the screen.  Any parameter can be selected from the drop-down list in the Cloth Controls dialog.  Do not by alarmed if the cloth should suddenly "explode", this is perfectly normal and means that you have chosen a parameter for which the default time step is too large.

Exporting Maya Scripts
To export to a Maya script, choose File->Save from the menu at the top of the screen.  A file selection dialog box will open up and allow you to specify the name of the object in Maya.  Choose a meaningful name and press the Save button.  A new dialog box will open up and allow you to specify the number of simulation steps to skip when constructing the animation, as well as the size of the cubic spline patch in Maya.  The default skip rate assumes Maya will be animating at 30 frames/sec.  Specify the number of spline patches in the u and v directions.  After pressing OK, the program will create two files: create_name.mel and animate_name.mel.  The simulation will progress with the window bar displaying the current frame number being recorded.  When you decide enough frames have been saved, choose File->Save another time to stop the recording.

Importing Into Maya
In Maya, execute create_name.mel from the script editor.  After this, execute animate_name.mel from the script editor.  (Patience is important here as the script files tend to be very large and thus take a long time to load and execute.)  Apply a pretty texture and enjoy the pretty curtains.